Exceptional Rings Unveiled: The New Frontier of Nonlinear Non-Hermitian Optical Microcavities
In a groundbreaking study, researchers have explored the intriguing concept of exceptional rings (ERs) in nonlinear non-Hermitian planar optical microcavities. This research, spearheaded by Jan Wingenbach and colleagues from various prestigious institutions, highlights how the interplay of light and nonlinear materials could lead to enhanced sensitivity and novel dynamical behaviors in optical systems.
Understanding Exceptional Points and Rings
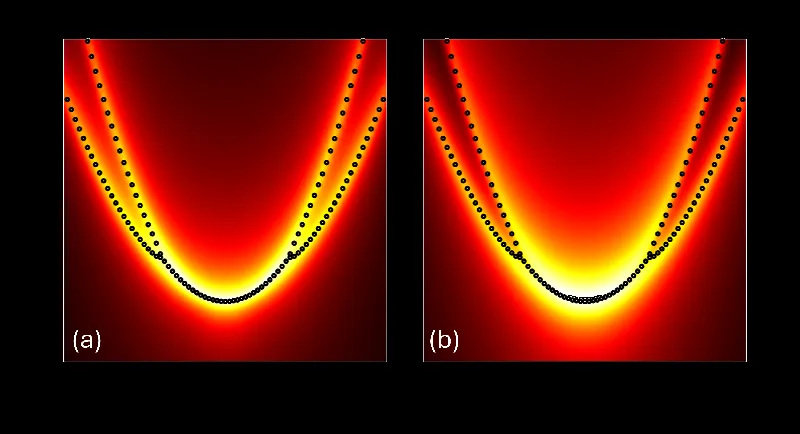
Exceptional points are unique conditions in a non-Hermitian system where two or more eigenvalues coalesce, leading to striking behaviors such as increased sensitivity to perturbations. Rings of exceptional points (ERs) form a continuous loop in the eigenvalue spectrum, marking a significant advancement from isolated points. When nonlinear effects are introduced, such as Kerr-type nonlinearity, the linear exceptional ring can split into multiple concentric rings, revealing a complex topological structure that has previously remained unexplored.
The Role of Nonlinearity
At the heart of this research is the introduction of nonlinear dynamics into planar optical resonators. By infusing a Kerr-type medium, researchers found that the exceptional ring splits into an inner ring of second-order exceptional points and an outer ring of third-order exceptional points. This splitting not only enriches the topology of the system but also enhances its sensitivity to variations, making it an exciting platform for practical applications such as high-precision sensors.
A Universal Framework for Non-Hermitian Systems
The findings from this study extend beyond the specific system investigated. The researchers argue that the discovered characteristics of ERs and their enhanced perturbation responses are applicable to a wide array of nonlinear non-Hermitian systems. This universal framework can pave the way for engineering exceptional points and rings in various physical contexts, potentially revolutionizing the design of optical devices.
Implications for Future Technologies
The implications of this research are profound. The enhanced perturbation response observed in nonlinear exceptional rings indicates a promising direction for sensor technology, where precision measurement at the level of exceptional points could vastly improve the efficacy of devices in fields ranging from medical diagnostics to environmental monitoring. Furthermore, the analysis of topological features in these systems opens new avenues for exploring quantum phenomena and fostering innovations in photonics.
As this frontier of research continues to unfold, the potential for harnessing nonlinear non-Hermitian systems in practical applications remains vast. The next steps will likely involve experimental realizations and real-world implementations of these intriguing optical structures.